Em primeiro lugar o cálculo das estatísticas descritivas depende da forma em que os dados disponíveis estão organizados. Se temos aceso à lista individual de todos os dados, então temos dados não classificados. Por outro lado, se temos acesso a uma distribuição de frequências, então os dados estão classificados. Neste contexto, iremos de seguida apresentar as estatísticas mais importantes para caracterizar um determinado fenómeno, distinguindo entre dados não classificados e dados classificados.
1. Média Aritmética
Dados classificados\(\rightarrow \bar{x}=\frac{1}{N}\sum \limits_{i=1}^N n_{i} x_{i}^{'}=\sum \limits_{i=1}^N f_{i} x_{i}^{'}\)
onde \(x_{i}^{'}=l_{i}+\frac{1}{2} h_{i}\) é o ponto médio de classe i.
Dados não classificados \(\rightarrow \bar{x}=\frac{1}{N}\sum \limits_{i=1}^N x_{i}\)
2. Mediana
Dados classificados: a mediana \((m_{e})\) é o valor que divide o conjunto dos dados em dois subconjuntos iguais.
\(s(m_{e})=s(Q2)=\frac{1}{2}\)
Dados não classificados e \(x_{1} < x_{2} < \dots < x_{N}\)
Se N ímpar, então \(N=2k+1\) com \(m_{e}=x_{k+1}\)
Se N par, então \(N=2k\) com \(m_{e}=\frac{x_{k}+x_{k+1}}{2}\)
Dados classificados\(\rightarrow\;mo=l_{mo}+\frac{f_{mo+1}}{f_{mo+1}+f_{mo-1}}h_{mo}\)
Dados não classificados: valor mais frequente.
Para um melhor estudo e caracterização das distribuições, consideram-se aqui um conjunto de valores separadores denominados Quantis. Estes valores dividem o conjunto das observações em subconjuntos iguais.
\(q_{\theta}\rightarrow Quantil\;de\;ordem\;\theta,\;em\;que\;0 < \theta < 1\)
Os quantis mais utilizados são os quartis, decis e percentis, que dividem, respectivamente, o conjunto ordenado de observações (variáveis discretas) ou a área do histograma (variáveis contínuas) em quatro, dez e cem partes iguais.
\(Dados\;não\;classificados\; e\:\; x_{1} < x_{2} < \dots < x_{N}\) Primeiro quartil (valor abaixo do qual estão 25% das observações e 75% acima).
\( \theta=\frac{1}{4}\rightarrow k=\frac{N+1}{4}\; em\;que\; q_{1}=x_{k}\)
Segundo quartil (valor abaixo do qual estão 50% das observações e 50% acima - mediana).
\(\theta=\frac{2}{4}\rightarrow k=\frac{N+1}{2}\; em\;que\; q_{2}=x_{k}\)
Terceiro quartil (valor abaixo do qual estão 75% das observações e 25% acima).
\( \theta=\frac{3}{4}\rightarrow k=\frac{3(N+1)}{4}\; em\;que\; q_{3}=x_{k}\)
Se k é um valor inteiro, então o valor observado indicado por k corresponde ao quartil.
Se k não é inteiro, então o valor do quartil pode ser calculado de duas formas:
(1) quando o valor de k está a igual distância de dois valores inteiros então o quantil correspondente é igual à média aritmética das observações indicadas por esses valores;
(2) quando se aproxima mais de um determinado valor inteiro, calcula-se k procedendo ao seu arredondamento para o inteiro mais próximo.
Dados\;classificados:
\(s(q_{\theta})=\theta\) Considerando o nosso exemplo anterior, nomeadamente a função cumulativa apresentada na distribuição de frequências das notas de entrada no curso, podemos representar graficamente o cálculo dos quartis.
Figura 4. Representação gráfica do cálculo dos quartis.
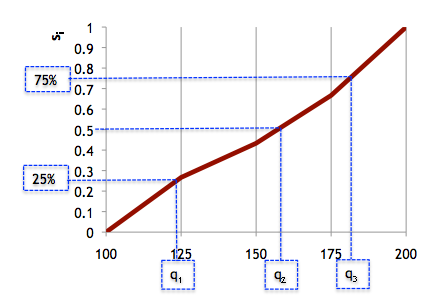
Assim:
1º quartil - s(q1) = 0.25
2º quartil - s(q2) = 0.5
3º quartil - s(q3) = 0.75
Trata-se portanto de calcular os valores, no eixo das abcissas, correspondentes às frequências acumuladas de 0.25, 0.5 e 0.75. Para o cálculo de q1 sabe-se que o seu valor pertence à classe 100 - 125, então:
$$s(100) = 0 < s(q_{1}) < s(125) = 0.26(6) $$ e por interpolação linear
$$\frac{q_{1}-100}{125-100}=\frac{0.25-0}{0.26(6)-0}$$ $$ q_{1}=123.4$$ Portanto, 25% dos alunos entraram no curso com uma nota inferior a 123.4, enquanto os restantes alunos (75%) entraram com uma nota superior.
Seguindo o mesmo método para o cálculo de q2 (mediana) e para o terceiro quartil, teremos:
$$\frac{q_{2}-150}{175-150}=\frac{0.5-0.43(3)}{0.66(6)-0.43(3)} $$ $$q_{2}=157.14$$ $$\frac{q_{3}-175}{200-175}=\frac{0.75-0.66(6)}{1-0.66(6)}$$ $$q_{3}=181.25$$ Figura 5. Representação gráfica do cálculo dos quartis.
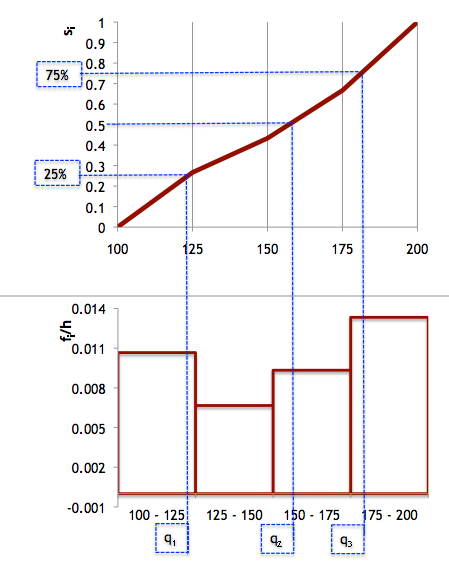
1. Amplitude total
\(AT=max(x_{i})-min(x_{i})\)
\(q=q_{3}-q_{1}\)
\(sq=\frac{q_{3}-q_{1}}{2}\)
\(Dados\;classificados\rightarrow d=\frac{1}{N}\sum \limits_{i=1}^kn_{i}|x_{i}^{'}-\bar{x}|\)
\(Dados\;não\;classificados\rightarrow d=\frac{1}{N}\sum \limits_{i=1}^N|x_{i}-\bar{x}|\)
\(Dados\;classificados\rightarrow s^{2}=\frac{1}{N}\sum \limits_{i=1}^kn_{i}(x_{i}^{'}-\bar{x})^{2}\)
\(Dados\;não\;classificados\rightarrow s^{2}=\frac{1}{N}\sum \limits_{i=1}^N(x_{i}-\bar{x})^{2}\)
\(s=\sqrt{s^{2}}\)
Quando N é pequeno utiliza-se a variância corrigida.
\(s'^{2}=\frac{1}{N-1}\sum \limits_{i=1}^N(x_{i}-\bar{x})^{2}\)
O coeficiente de variação é uma medida de dispersão relativa, ou seja, é independente, quer das unidades de medida quer das escalas, com que os dados são medidos. A eliminação destes factores (unidades de medida e escala), faz com que esta medida seja utilizada na comparação da dispersão de dois ou mais conjuntos de dados.
$$cv =\frac{s}{\bar{x}}100$$
MEDIDAS DE LOCALIZÇÃO
1. Média Aritmética
Dados classificados\(\rightarrow \bar{x}=\frac{1}{N}\sum \limits_{i=1}^N n_{i} x_{i}^{'}=\sum \limits_{i=1}^N f_{i} x_{i}^{'}\)
onde \(x_{i}^{'}=l_{i}+\frac{1}{2} h_{i}\) é o ponto médio de classe i.
Dados não classificados \(\rightarrow \bar{x}=\frac{1}{N}\sum \limits_{i=1}^N x_{i}\)
2. Mediana
Dados classificados: a mediana \((m_{e})\) é o valor que divide o conjunto dos dados em dois subconjuntos iguais.
\(s(m_{e})=s(Q2)=\frac{1}{2}\)
Dados não classificados e \(x_{1} < x_{2} < \dots < x_{N}\)
Se N ímpar, então \(N=2k+1\) com \(m_{e}=x_{k+1}\)
Se N par, então \(N=2k\) com \(m_{e}=\frac{x_{k}+x_{k+1}}{2}\)
3. Moda
Dados classificados\(\rightarrow\;mo=l_{mo}+\frac{f_{mo+1}}{f_{mo+1}+f_{mo-1}}h_{mo}\)
Dados não classificados: valor mais frequente.
4.Quantis
Para um melhor estudo e caracterização das distribuições, consideram-se aqui um conjunto de valores separadores denominados Quantis. Estes valores dividem o conjunto das observações em subconjuntos iguais.
\(q_{\theta}\rightarrow Quantil\;de\;ordem\;\theta,\;em\;que\;0 < \theta < 1\)
Os quantis mais utilizados são os quartis, decis e percentis, que dividem, respectivamente, o conjunto ordenado de observações (variáveis discretas) ou a área do histograma (variáveis contínuas) em quatro, dez e cem partes iguais.
\(Dados\;não\;classificados\; e\:\; x_{1} < x_{2} < \dots < x_{N}\) Primeiro quartil (valor abaixo do qual estão 25% das observações e 75% acima).
\( \theta=\frac{1}{4}\rightarrow k=\frac{N+1}{4}\; em\;que\; q_{1}=x_{k}\)
Segundo quartil (valor abaixo do qual estão 50% das observações e 50% acima - mediana).
\(\theta=\frac{2}{4}\rightarrow k=\frac{N+1}{2}\; em\;que\; q_{2}=x_{k}\)
Terceiro quartil (valor abaixo do qual estão 75% das observações e 25% acima).
\( \theta=\frac{3}{4}\rightarrow k=\frac{3(N+1)}{4}\; em\;que\; q_{3}=x_{k}\)
Se k é um valor inteiro, então o valor observado indicado por k corresponde ao quartil.
Se k não é inteiro, então o valor do quartil pode ser calculado de duas formas:
(1) quando o valor de k está a igual distância de dois valores inteiros então o quantil correspondente é igual à média aritmética das observações indicadas por esses valores;
(2) quando se aproxima mais de um determinado valor inteiro, calcula-se k procedendo ao seu arredondamento para o inteiro mais próximo.
Dados\;classificados:
\(s(q_{\theta})=\theta\) Considerando o nosso exemplo anterior, nomeadamente a função cumulativa apresentada na distribuição de frequências das notas de entrada no curso, podemos representar graficamente o cálculo dos quartis.
Figura 4. Representação gráfica do cálculo dos quartis.

Assim:
1º quartil - s(q1) = 0.25
2º quartil - s(q2) = 0.5
3º quartil - s(q3) = 0.75
Trata-se portanto de calcular os valores, no eixo das abcissas, correspondentes às frequências acumuladas de 0.25, 0.5 e 0.75. Para o cálculo de q1 sabe-se que o seu valor pertence à classe 100 - 125, então:
$$s(100) = 0 < s(q_{1}) < s(125) = 0.26(6) $$ e por interpolação linear
$$\frac{q_{1}-100}{125-100}=\frac{0.25-0}{0.26(6)-0}$$ $$ q_{1}=123.4$$ Portanto, 25% dos alunos entraram no curso com uma nota inferior a 123.4, enquanto os restantes alunos (75%) entraram com uma nota superior.
Seguindo o mesmo método para o cálculo de q2 (mediana) e para o terceiro quartil, teremos:
$$\frac{q_{2}-150}{175-150}=\frac{0.5-0.43(3)}{0.66(6)-0.43(3)} $$ $$q_{2}=157.14$$ $$\frac{q_{3}-175}{200-175}=\frac{0.75-0.66(6)}{1-0.66(6)}$$ $$q_{3}=181.25$$ Figura 5. Representação gráfica do cálculo dos quartis.

MEDIDAS DE DISPERSÃO
1. Amplitude total
\(AT=max(x_{i})-min(x_{i})\)
2. Amplitude inter-quartil
\(q=q_{3}-q_{1}\)
3. Amplitude semi-quartil
\(sq=\frac{q_{3}-q_{1}}{2}\)
4. Desvio médio
\(Dados\;classificados\rightarrow d=\frac{1}{N}\sum \limits_{i=1}^kn_{i}|x_{i}^{'}-\bar{x}|\)
\(Dados\;não\;classificados\rightarrow d=\frac{1}{N}\sum \limits_{i=1}^N|x_{i}-\bar{x}|\)
5. Variância e desvio padrão
\(Dados\;classificados\rightarrow s^{2}=\frac{1}{N}\sum \limits_{i=1}^kn_{i}(x_{i}^{'}-\bar{x})^{2}\)
\(Dados\;não\;classificados\rightarrow s^{2}=\frac{1}{N}\sum \limits_{i=1}^N(x_{i}-\bar{x})^{2}\)
\(s=\sqrt{s^{2}}\)
Quando N é pequeno utiliza-se a variância corrigida.
\(s'^{2}=\frac{1}{N-1}\sum \limits_{i=1}^N(x_{i}-\bar{x})^{2}\)
6. Coeficiente de variação
O coeficiente de variação é uma medida de dispersão relativa, ou seja, é independente, quer das unidades de medida quer das escalas, com que os dados são medidos. A eliminação destes factores (unidades de medida e escala), faz com que esta medida seja utilizada na comparação da dispersão de dois ou mais conjuntos de dados.
$$cv =\frac{s}{\bar{x}}100$$