Uma estatística é uma medida de um atributo presente em várias unidades estatísticas, é portanto uma condensação, uma síntese, de um conjunto de informação maior. Uma das formas mais simples, e bastante eficaz, de agregarmos dados para obtermos informação mais relevante sob determinada perspectiva é através da construção de quadros (ou distribuições) de frequências. Frequência absoluta - número de vezes que um acontecimento ou fenómeno é observado. No caso da variável ser discreta teremos então k valores, ou k modalidades no caso da variável qualitativa, \(m_1, m_2, ..., m_k\) . Num conjunto de N observações \(x_1, x_2, ..., x_N\), é possível contar quantas satisfazem um determinado critério. Por exemplo, num curso de informática com 30 estudantes (N = 30) é possível calcular o número de alunos que foram excluidos, admitidos, ou dispensados da realização de um determinado exame, neste caso a variável qualitativa resultado da avaliação tem apenas três modalidades (k = 3): m1 = excluído, m2 = admitido e m3 = dispensado. Esta contagem pode ser formalizada da seguinte forma: $$n_{i}=\sharp \left \{ x_{j} ={m_{i}}\left ( j=1,2,...,N\right )\right \}$$ onde $$\sum_{i=1}^{k} n_{i}=N$$ Frequência relativa: é número de vezes que um acontecimento ou fenómeno é observado em relação ao número total de observações (N). É portanto a proporção entre os acontecimentos que consideramos favoráveis e o total. $$f_{i}=\frac{n_{i}}{N} $$ e portanto $$ \sum_{i=1}^k f_{i}=1$$. Frequência (absoluta ou relativa) acumulada: representa o número (ou a proporção) total que os acontecimentos ou os fenómenos são observados. $$S_{i}=\sum \limits_{j=1}^{i} n_{j}=n_{1}+n_{2}+...+n_{i}$$ $$s_{i}=\sum_{j=1}^{i} f_{j} =f_{1}+f_{2}+...+f_{i}$$ Combinando estes conceitos numa tabela podemos apresentar os dados sob a forma de distribuições (ou quadros) de frequência. Se a variável em causa for qualitativa ou quantitativa discreta, então é possível enumerar os respectivos valores e obter a frequência com que ocorrem no nosso universo. Tomemos outra vez como exemplo o curso de informática com 30 alunos, sabendo agora que é composto por 6 alunos que foram excluídos de exame, 9 admitidos e 15 dispensados. Se esta informação tiver sido recolhida através de um inquérito (questionário) individual então será normal que a variável resultado da avaliação seja codificada (registada) da seguinte forma 1 - excluído, 2 - admitido, 3 - dispensado. Neste caso, os dados recolhidos podem ser apresentados sob a forma de lista 1,2,2,3,3, ...,2,1 (30 observações), ou sob forma de uma distribuição de frequências (quadro 1).

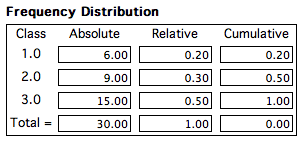
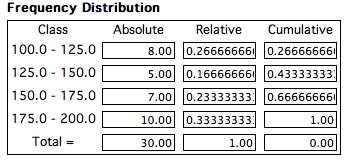
No quadro anterior verifica.se facilmente que os 9 alunos admitidos a exame correspondem a 30% do total e em conjunto com os 6 alunos excluídos representam 50%. Esta vantagem de termos a informação resumida pode perder-se se a variável for contínua ou se a variável discreta apresentar um elevado número de valores diferentes. Consideremos agora, para os mesmos alunos, a nota de entrada para o curso numa escala de 1 a 100. Admite-se facilmente que é pouco provável 2 ou 3 alunos terem exactamente a mesma nota de entrada. Neste caso o número de classes com apenas uma frequência será grande e a distribuição de frequências perde interesse. Em situações destas será conveniente definir classes com base em intervalos. Um algoritmo possível consiste em definir m classes (intervalos-\(I\)) de igual amplitude e podemos formalizar da seguinte forma: $$I_{1}=\left [l_{1}, l_{2} \right [\;\; I_{2}=\left [l_{2}, l_{3} \right [\;\cdots\; I_{m}=\left [l_{m}, l_{m+1} \right ]; l_{i} < l_{j};i < j$$ $$l_{1}\leq min\,x_{i};l_{m+1}\geq max\,x_{i} $$ $$1) I_{i} \cap I_{p}=\phi$$ $$2) \bigcup_{j=1}^{m} I_{j} \supset D, com \; D = \left [ min(x_{i}), max(x_{i}) \right ]$$ Portanto, a construção dos intervalos depende do número de classes e da amplitude de cada intervalo: $$Amplitude\, total = l_{m+1}-l_{1} $$ e $$h = \frac{l_{m+1}-l_{1}}{m}$$ A aplicação deste algoritmo às notas de entrada dos 30 alunos obtém-se o quadro 2.