Experiência aleatória e acontecimentos
A teoria da probabilidade teve o seu início no século XVII, em França, com dois grandes matemáticos: Blaise Pascal e Pierre de Fermat, na procura de respostas aos problemas colocados pelos jogos de fortuna e azar. Hoje em dia a teoria desempenha um papel crescente em muitas áreas: seguros, mercados, stocks, call-centers, etc. É um ramo da matemática que lida com as propriedades dos fenómenos onde o 'azar' intervém.
Na estatística, a teoria das probabilidades é utilizada em três domínios diferentes:
- a observação de dados estatísticos pode dar origem a valores errados (por exemplo, a utilização de um equipamento deficiente na medição da poluição de um rio). A teoria das probabilidades permite representar, através de variáveis aleatórias, os desvios entre os valores observados e os valores reais.
- o estudo de determinados fenómenos tem mostrado que a distribuição de uma determinada variável, numa população, está próxima de modelos probabilísticos;
- os métodos de amostragem aleatórios que permitem assegurar na amostra uma representatividade do universo num determinado critério relevante.
A definição clássica de probabilidade é portanto a relação entre o número de casos favoráveis ao acontecimento e o número total de casos possíveis, supondo todos os casos igualmente possíveis. Nesta experiência aleatória os casos possíveis são a cara ou a coroa e por conseguinte a Prob. cara = Prob. coroa = \(\frac{1}{2}\). Se em vez de um lançamento, efectuarmos dois lançamentos consecutivos da mesma moeda, então \(\Omega=\{(cara, cara), (cara, coroa), (coroa, cara), (coroa, coroa)\}\) e a probabilidade para que apareça apenas uma cara será de \( \frac{2}{4}=\frac{1}{2}\).
Portanto, usando a notação dos conjuntos, o acontecimento \(A\) é um subconjunto de resultados possíveis de uma experiência aleatória, \(A \subset \Omega \). Podemos por isso definir o conjunto de acontecimentos como uma família de subconjuntos, denominada \(\mathcal{A}\), onde se verificam os seguintes axiomas da álgebra de conjuntos:
1) \( \Omega \in \mathcal{A} \)
2) Se \(A \in \mathcal{A} \) então \( \bar{A} \in \mathcal{A} \)
A todo o acontecimento \(A\) podemos associar o seu contrário, denominado \( \bar{A}\), tal que se A se realiza então \( \bar{A}\) não, e reciprocamente. No contexto de \( \Omega \), \( \bar{A}\) é a parte complementar de \(A\).
3) Se \(A \in \mathcal{A}\) e \(B \in \mathcal{A}\) então \( A \cup B \in \mathcal{A} \)
Pode-se também mostrar que estes axiomas implicam também que o conjunto vazio \( \phi \in \mathcal{A} \) e que \( \cap A_{i} \in \mathcal{A} \).
O espaço de acontecimentos define-se por isso como o par \((\Omega, \mathcal{A})\), onde \(\Omega\) é o espaço de resultados e os seus subconjuntos estão em \( \mathcal{A}\).
A cada acontecimento podemos associar uma probabilidade compreendida entre 0 e 1. A teoria moderna das probabilidades assenta num conjunto de axiomas, geralmente conhecido pela Axiomática de Kolmogorov.
1) \(P(A) \geq 0 \), qualquer que seja o acontecimento \(A \in \mathcal{A}\)
2) \(P(\Omega) = 1\)
3) Se A e B são acontecimentos disjuntos (incompatíveis), i. e. \(A \cap B = \phi\), então \(P(A \cup B) = P(A) + P(B)\).
4) Se \(A_{1}, A_{2}, ... \)são acontecimentos disjuntos dois a dois, então
$$ P\left(\bigcup_{i=1}^{\infty} A_{i}\right)= \sum_{i=1}^{\infty}P(A_{i})$$
1) \(P(\bar{A}) = 1- P(A)\)
2) \(P(\phi) = 0 \)
3) \( P(A) \leq P(B) \) se \(A \subset B \)
4) \(P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
5) \(P(A - B) = P(A) - P(A \cap B) \)
O conceito de probabilidade condicional surge quando pretendemos reavaliar a probabilidade através da incorporação de nova informação. Suponhamos que nos interessa a realização de um acontecimento A, sabendo que um outro acontecimento B já se realizou. Se A e B são incompatíveis a questão está resolvida: A não se realizará. Se \(A \cap B \neq \phi \) então é possível que A se realize embora o universo de possibilidades não seja agora \( \Omega \), mas sim B.
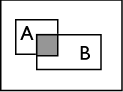
Com efeito, só interessa a realização de A no contexto de B. Ou seja, a probabilidade condicional de A dado B é $$ P(A|B) = \frac{P(A \cap B)}{P(B)} se P(B) >0$$ e portanto \(P(A \cap B) = P(A|B)P(B) \).
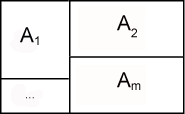 Diz-se que a classe de acontecimentos \(A_1, A_2, …, A_m \) é uma partição de \(\Omega\) quando
Diz-se que a classe de acontecimentos \(A_1, A_2, …, A_m \) é uma partição de \(\Omega\) quando
$$1) A_i \cap A_j = \phi, i \neq j$$ $$2) \bigcup_{i=1}^{m} A_{i} = \Omega$$ Por conseguinte,
$$ P\left(\bigcup_{i=1}^{m} A_{i}\right)= \sum_{i=1}^{m}P(A_{i})=1$$ Se \(A_i\) constituir um sistema completo de acontecimentos (uma partição de \(\Omega\) ) podemos escrever \(P(A_i \cap B)=P(A_i)(B|A_i)\) e o teorema das probabilidades totais $$ P(B)= \sum_{i=1}^{m}P(A_{i})P(B|A_{i})$$ O Teorema de Bayes será portanto enunciado da seguinte forma:
Se \(\{A_1, A_2, …, A_m\}\) é uma partição de \(\Omega\) e se \(P(A_i) > 0, i=1,2,…,m\) então dado qualquer acontecimento, \(B\), com \(P(B) > 0\) e $$P(A_{i}|B) = \frac{P(A_{i})P(B|A_{i})}{P(B)}, i=1,2,...,m$$
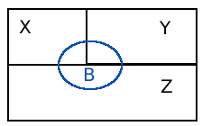 $$P(X) = 0.2 , P(Y) = 0.3 , P(Z) = 0.5$$
$$P(B|X) = 0.05 , P(B|Y) = 0.1 , P(B|Z) = 0.15 $$
Neste contexto, se tirarmos ao acaso um artigo produzido nesta fábrica, a probabilidade de que seja defeituoso corresponde ao cálculo da probabilidade total, uma vez que
$$ P(B) = P(X)P(B|X)+ P(Y)P(B|Y)+ P(Z)P(B|Z) = 0.2\times 0.05 + 0.3\times 0.1 + 0.5\times 0.15 = 0.115$$
Sabendo agora que o artigo é defeituoso as probabilidades desse artigo ter sido inspeccionado por X, Y ou Z são dadas por:
$$P(X|B) = \frac{P(X)P(B|X)}{P(B)}=\frac{0.2\times 0.05}{0.115}=0.087$$
$$P(Y|B) = \frac{P(Y)P(B|Y)}{P(B)}=\frac{0.3\times 0.1}{0.115}=0.26$$
$$P(Z|B) = \frac{P(Z)P(B|Z)}{P(B)} = \frac{0.5\times 0.15}{0.115}=0.652$$
São denominadas probabilidades a posteriori porque sabemos primeiro que o artigo é defeituoso e só depois a probabilidade de ser inspeccionado por um dos inspectores. Não devemos portanto confundir a probabilidade condicionada com a probabilidade a posteriori porque este caso é a probabilidade do artigo ser defeituoso quando inspeccionado por um determinado inspector.
$$P(X) = 0.2 , P(Y) = 0.3 , P(Z) = 0.5$$
$$P(B|X) = 0.05 , P(B|Y) = 0.1 , P(B|Z) = 0.15 $$
Neste contexto, se tirarmos ao acaso um artigo produzido nesta fábrica, a probabilidade de que seja defeituoso corresponde ao cálculo da probabilidade total, uma vez que
$$ P(B) = P(X)P(B|X)+ P(Y)P(B|Y)+ P(Z)P(B|Z) = 0.2\times 0.05 + 0.3\times 0.1 + 0.5\times 0.15 = 0.115$$
Sabendo agora que o artigo é defeituoso as probabilidades desse artigo ter sido inspeccionado por X, Y ou Z são dadas por:
$$P(X|B) = \frac{P(X)P(B|X)}{P(B)}=\frac{0.2\times 0.05}{0.115}=0.087$$
$$P(Y|B) = \frac{P(Y)P(B|Y)}{P(B)}=\frac{0.3\times 0.1}{0.115}=0.26$$
$$P(Z|B) = \frac{P(Z)P(B|Z)}{P(B)} = \frac{0.5\times 0.15}{0.115}=0.652$$
São denominadas probabilidades a posteriori porque sabemos primeiro que o artigo é defeituoso e só depois a probabilidade de ser inspeccionado por um dos inspectores. Não devemos portanto confundir a probabilidade condicionada com a probabilidade a posteriori porque este caso é a probabilidade do artigo ser defeituoso quando inspeccionado por um determinado inspector.
Um exemplo que nos permite ver os dois lados desta moeda é o do comerciante que recebe batata de três regiões diferentes. Ao chegar, cada lote é classificado em duas classes A e B, de acordo com a qualidade do produto. Neste momento a distribuição dos lotes recebidos até à data é a seguinte:
$$\newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|c|c|c|c|} \hline & & Qualidade \\\hline Regiões & KG & A \hspace{2 cm} B \\\hline I & 10000 &2000 \hspace{1.5 cm} 8000 \\\hline II & 20000 & 14000 \hspace{1.5 cm} 6000 \\\hline III & 20000 & 10000 \hspace{1.5 cm} 10000 \\\hline & 50000 & \\\hline \end{array} $$
A teoria da probabilidade teve o seu início no século XVII, em França, com dois grandes matemáticos: Blaise Pascal e Pierre de Fermat, na procura de respostas aos problemas colocados pelos jogos de fortuna e azar. Hoje em dia a teoria desempenha um papel crescente em muitas áreas: seguros, mercados, stocks, call-centers, etc. É um ramo da matemática que lida com as propriedades dos fenómenos onde o 'azar' intervém.
Na estatística, a teoria das probabilidades é utilizada em três domínios diferentes:
- a observação de dados estatísticos pode dar origem a valores errados (por exemplo, a utilização de um equipamento deficiente na medição da poluição de um rio). A teoria das probabilidades permite representar, através de variáveis aleatórias, os desvios entre os valores observados e os valores reais.
- o estudo de determinados fenómenos tem mostrado que a distribuição de uma determinada variável, numa população, está próxima de modelos probabilísticos;
- os métodos de amostragem aleatórios que permitem assegurar na amostra uma representatividade do universo num determinado critério relevante.
Este ramo autónomo da matemática, que permite o desenvolvimento de teorias probabilísticas, baseia-se numa axiomática própria que modela os resultados obtidos na realização de experiências aleatórias. Uma experiência, diz-se aleatória se não podemos prever o seu resultado antecipadamente, mesmo que essa experiência se repita em condições idênticas. No entanto, apesar de não ser possível prever o resultado, podemos representar o conjunto de todos os resultados possíveis: \(\Omega\). Portanto, \(\Omega\) é o conjunto fundamental (não vazio), discreto ou contínuo, formado por todos os resultados que é possível obter quando se efectua a experiência aleatória. Por exemplo, uma experiência aleatória que consiste no lançamento ao ar de uma moeda perfeita tem associada o seguinte conjunto \(\Omega=\{cara, coroa\}\).
A definição clássica de probabilidade é portanto a relação entre o número de casos favoráveis ao acontecimento e o número total de casos possíveis, supondo todos os casos igualmente possíveis. Nesta experiência aleatória os casos possíveis são a cara ou a coroa e por conseguinte a Prob. cara = Prob. coroa = \(\frac{1}{2}\). Se em vez de um lançamento, efectuarmos dois lançamentos consecutivos da mesma moeda, então \(\Omega=\{(cara, cara), (cara, coroa), (coroa, cara), (coroa, coroa)\}\) e a probabilidade para que apareça apenas uma cara será de \( \frac{2}{4}=\frac{1}{2}\).
Por outro lado, a probabilidade pode ser interpretada como uma frequência relativa (Interpretação frequencista): a probabilidade de um acontecimento pode ser medida através da observação da frequência relativa do mesmo acontecimento num grande conjunto de provas ou experiências, idênticas e independentes (“lei dos grandes números”). $$f_{N}(A)=\frac{n_{N}(A)}{N} $$ A frequência relativa com a qual o acontecimento A ocorre, flutuará menos à medida que o tempo passa, tenderá para o limite à medida que N aumenta. Exemplo: (%) de Alunos e Alunas na sala. Ou o nascimento de bebés do sexo masculino e feminino.
Neste contexto um acontecimento é uma proposição lógica relativa ao resultado da experiência. O acontecimento só se realiza, ou não, consoante a proposição seja verdadeira, ou falsa, depois de terminada a experiência. À realização de um acontecimento podemos associar todos os resultados correspondentes. No exemplo anterior, a saída de pelo menos uma cara corresponde ao conjunto seguinte: \( \{(cara, coroa), (coroa, cara)\} \), ou seja, uma parte de \( \Omega \).
Álgebra de acontecimentos
Portanto, usando a notação dos conjuntos, o acontecimento \(A\) é um subconjunto de resultados possíveis de uma experiência aleatória, \(A \subset \Omega \). Podemos por isso definir o conjunto de acontecimentos como uma família de subconjuntos, denominada \(\mathcal{A}\), onde se verificam os seguintes axiomas da álgebra de conjuntos:
1) \( \Omega \in \mathcal{A} \)
2) Se \(A \in \mathcal{A} \) então \( \bar{A} \in \mathcal{A} \)
A todo o acontecimento \(A\) podemos associar o seu contrário, denominado \( \bar{A}\), tal que se A se realiza então \( \bar{A}\) não, e reciprocamente. No contexto de \( \Omega \), \( \bar{A}\) é a parte complementar de \(A\).
3) Se \(A \in \mathcal{A}\) e \(B \in \mathcal{A}\) então \( A \cup B \in \mathcal{A} \)
Pode-se também mostrar que estes axiomas implicam também que o conjunto vazio \( \phi \in \mathcal{A} \) e que \( \cap A_{i} \in \mathcal{A} \).
O espaço de acontecimentos define-se por isso como o par \((\Omega, \mathcal{A})\), onde \(\Omega\) é o espaço de resultados e os seus subconjuntos estão em \( \mathcal{A}\).
Espaço de probabilidade
A cada acontecimento podemos associar uma probabilidade compreendida entre 0 e 1. A teoria moderna das probabilidades assenta num conjunto de axiomas, geralmente conhecido pela Axiomática de Kolmogorov.
1) \(P(A) \geq 0 \), qualquer que seja o acontecimento \(A \in \mathcal{A}\)
2) \(P(\Omega) = 1\)
3) Se A e B são acontecimentos disjuntos (incompatíveis), i. e. \(A \cap B = \phi\), então \(P(A \cup B) = P(A) + P(B)\).
4) Se \(A_{1}, A_{2}, ... \)são acontecimentos disjuntos dois a dois, então
$$ P\left(\bigcup_{i=1}^{\infty} A_{i}\right)= \sum_{i=1}^{\infty}P(A_{i})$$
Como consequência desta axiomática, podemos também enunciar as propriedades seguintes:
1) \(P(\bar{A}) = 1- P(A)\)
2) \(P(\phi) = 0 \)
3) \( P(A) \leq P(B) \) se \(A \subset B \)
4) \(P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
5) \(P(A - B) = P(A) - P(A \cap B) \)
Probabilidade condicional e independência
O conceito de probabilidade condicional surge quando pretendemos reavaliar a probabilidade através da incorporação de nova informação. Suponhamos que nos interessa a realização de um acontecimento A, sabendo que um outro acontecimento B já se realizou. Se A e B são incompatíveis a questão está resolvida: A não se realizará. Se \(A \cap B \neq \phi \) então é possível que A se realize embora o universo de possibilidades não seja agora \( \Omega \), mas sim B.

Com efeito, só interessa a realização de A no contexto de B. Ou seja, a probabilidade condicional de A dado B é $$ P(A|B) = \frac{P(A \cap B)}{P(B)} se P(B) >0$$ e portanto \(P(A \cap B) = P(A|B)P(B) \).
Se A e B são independentes, então \(P(A|B) = P(A) \) e \(P(B|A) = P(B) \). Neste sentido, \(P(A \cap B) = P(A)P(B)\).
Teorema de Bayes Seja o seguinte espaço amostral \( \Omega = \{A_1, A_2, ..., A_m \}\)
 Diz-se que a classe de acontecimentos \(A_1, A_2, …, A_m \) é uma partição de \(\Omega\) quando
Diz-se que a classe de acontecimentos \(A_1, A_2, …, A_m \) é uma partição de \(\Omega\) quando$$1) A_i \cap A_j = \phi, i \neq j$$ $$2) \bigcup_{i=1}^{m} A_{i} = \Omega$$ Por conseguinte,
$$ P\left(\bigcup_{i=1}^{m} A_{i}\right)= \sum_{i=1}^{m}P(A_{i})=1$$ Se \(A_i\) constituir um sistema completo de acontecimentos (uma partição de \(\Omega\) ) podemos escrever \(P(A_i \cap B)=P(A_i)(B|A_i)\) e o teorema das probabilidades totais $$ P(B)= \sum_{i=1}^{m}P(A_{i})P(B|A_{i})$$ O Teorema de Bayes será portanto enunciado da seguinte forma:
Se \(\{A_1, A_2, …, A_m\}\) é uma partição de \(\Omega\) e se \(P(A_i) > 0, i=1,2,…,m\) então dado qualquer acontecimento, \(B\), com \(P(B) > 0\) e $$P(A_{i}|B) = \frac{P(A_{i})P(B|A_{i})}{P(B)}, i=1,2,...,m$$
Tomemos como exemplo uma fábrica onde 3 inspectores X, Y e Z inspeccionam 20%, 30% e 50% dos artigos produzidos. Ou seja, todos os artigos produzidos são inspeccionados e ao seleccionarmos aleatoriamente um, a probabilidade desse artigo ter sido inspeccionado por X é 0.2 , por Y é 0.3 e por Z é 0.5. Neste universo de artigos existem naturalmente artigos defeituosos que são inspeccionados\detectados pelos três inspectores. Com base no histórico sabemos que cada inspector detecta uma determinada percentagem de artigos defeituosos. Assim, o inspector X de todos os artigos que inspecciona encontra apenas 5% de artigos defeituosos, enquanto Y e Z detectam 10% e 15%, respectivamente. Nesta partição de \( \Omega\) ocorre também B - artigo defeituoso e a probabilidade de serem detectados artigos defeituosos naqueles que são inspeccionados por X, Y e Z é igual a 0.05, 0.1 ou 0.15, respectivamente.
 $$P(X) = 0.2 , P(Y) = 0.3 , P(Z) = 0.5$$
$$P(B|X) = 0.05 , P(B|Y) = 0.1 , P(B|Z) = 0.15 $$
Neste contexto, se tirarmos ao acaso um artigo produzido nesta fábrica, a probabilidade de que seja defeituoso corresponde ao cálculo da probabilidade total, uma vez que
$$ P(B) = P(X)P(B|X)+ P(Y)P(B|Y)+ P(Z)P(B|Z) = 0.2\times 0.05 + 0.3\times 0.1 + 0.5\times 0.15 = 0.115$$
Sabendo agora que o artigo é defeituoso as probabilidades desse artigo ter sido inspeccionado por X, Y ou Z são dadas por:
$$P(X|B) = \frac{P(X)P(B|X)}{P(B)}=\frac{0.2\times 0.05}{0.115}=0.087$$
$$P(Y|B) = \frac{P(Y)P(B|Y)}{P(B)}=\frac{0.3\times 0.1}{0.115}=0.26$$
$$P(Z|B) = \frac{P(Z)P(B|Z)}{P(B)} = \frac{0.5\times 0.15}{0.115}=0.652$$
São denominadas probabilidades a posteriori porque sabemos primeiro que o artigo é defeituoso e só depois a probabilidade de ser inspeccionado por um dos inspectores. Não devemos portanto confundir a probabilidade condicionada com a probabilidade a posteriori porque este caso é a probabilidade do artigo ser defeituoso quando inspeccionado por um determinado inspector.
$$P(X) = 0.2 , P(Y) = 0.3 , P(Z) = 0.5$$
$$P(B|X) = 0.05 , P(B|Y) = 0.1 , P(B|Z) = 0.15 $$
Neste contexto, se tirarmos ao acaso um artigo produzido nesta fábrica, a probabilidade de que seja defeituoso corresponde ao cálculo da probabilidade total, uma vez que
$$ P(B) = P(X)P(B|X)+ P(Y)P(B|Y)+ P(Z)P(B|Z) = 0.2\times 0.05 + 0.3\times 0.1 + 0.5\times 0.15 = 0.115$$
Sabendo agora que o artigo é defeituoso as probabilidades desse artigo ter sido inspeccionado por X, Y ou Z são dadas por:
$$P(X|B) = \frac{P(X)P(B|X)}{P(B)}=\frac{0.2\times 0.05}{0.115}=0.087$$
$$P(Y|B) = \frac{P(Y)P(B|Y)}{P(B)}=\frac{0.3\times 0.1}{0.115}=0.26$$
$$P(Z|B) = \frac{P(Z)P(B|Z)}{P(B)} = \frac{0.5\times 0.15}{0.115}=0.652$$
São denominadas probabilidades a posteriori porque sabemos primeiro que o artigo é defeituoso e só depois a probabilidade de ser inspeccionado por um dos inspectores. Não devemos portanto confundir a probabilidade condicionada com a probabilidade a posteriori porque este caso é a probabilidade do artigo ser defeituoso quando inspeccionado por um determinado inspector.Um exemplo que nos permite ver os dois lados desta moeda é o do comerciante que recebe batata de três regiões diferentes. Ao chegar, cada lote é classificado em duas classes A e B, de acordo com a qualidade do produto. Neste momento a distribuição dos lotes recebidos até à data é a seguinte:
$$\newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|c|c|c|c|} \hline & & Qualidade \\\hline Regiões & KG & A \hspace{2 cm} B \\\hline I & 10000 &2000 \hspace{1.5 cm} 8000 \\\hline II & 20000 & 14000 \hspace{1.5 cm} 6000 \\\hline III & 20000 & 10000 \hspace{1.5 cm} 10000 \\\hline & 50000 & \\\hline \end{array} $$